Set Theory - Introduction to discrete mathematics
the fundamental concept of sets, functions, logic, graphs, trees, relations,
combinatorics, mathematical induction, and recursive relations.
Syllabus
Webinar
Review before the midterm and final exam!
What is the definition of Sets?
A set is a collection of distinct items. Sets are used to study a relation between object members in a particular domain. [reference 1]
collection of objects.
Mathematicians use, the term is set to refer to a well-defined, unordered, collection of any kind of object, duplicates are allowed.
The empty set is a set that contains nothing.
Examples
vowels V = {a,e,i,o,u}
Definition:
$$ A \subseteq B \iff x \in A \ \implies \ x \in B $$
$$ \therefore N \subseteq Z \subseteq Q \subseteq \mathbb{R} $$
$ S_4 = \{ \frac{1}{2}, \frac{1}{4}, \frac{1}{6}, \frac{1}{8}, \frac{1}{10} \} \implies $$ S_4 = \{ \frac{1}{2*1}, \frac{1}{2*2}, \frac{1}{2*3}, \frac{1}{2*4} , \frac{1}{2*5} \} \implies $
given a set S={1, 2, 3},
Given a set A, if |A| = n, find |P(P(P(A)))| :
$ 2^2 = 4 $
$ 2^3 = 8 $
$ 2^4 = 16 $
$ 2^5 = 32 $
$ 2^6 = 64 $
$ 2^7 = 128 $
$ 2^8 = 256 $
$ 2^9 = 512 $
$ 2^{10} = 1,024 $
Example:
$ A \cap \overline{ \overline{A} \cup \overline{B}} = A \cap \{2\} = \{1, 2\} \cap \{2\} = \{2\} $
$ \{2\} = A \cap B $
Exercise:
Given two sets A and B,
$$ \overline{ \overline{ A} \cup \overline{ B} } = A \cap B $$
$ A - \overline{B} = \{1, 2 \} - \{ 1, 4 \} = {4} = \overline{ A \cup B}$
Tip: Q.E.D. QUOD ERAT DEMONSTRANDUM means "Which was to be demonstrated."
Exercise
Given three sets A, B, and C, prove that:
Discrete Mathematics with Applications
Thomas Koshy
pp.70-71, 71-73, and 78-86.
Please also complete the following exercises:
pp.93, exercises 5–14, 27-32, and 57-60.
empty set E = {} = $ \emptyset $ or $ \varnothing $
Set notation
- an element of a set
- belongs in $ \in $
- not belong in $ \notin $
- the cardinality of a set
- Definition: Given a set S, the cardinality of S is the number of elements contained in S. We write the cardinality of S as |S|.
- Given V = {a,e,i,o,u}; |V| = 5
- |E| = |{}| = $ | \emptyset | $ = $ | \varnothing | $ = 0
Subset
- A is a subset of B if every element of A also belongs to B.
- A is also an element of B. $ A \subseteq B $
- subset \subset
- not subset equal $ \not \subseteq$
- subset not equal $ \subsetneqq $
- subset not equal $ \subsetneq $
- if V = {a,e,i,o,u} AND W={u,w}$ \implies W \subsetneq V $
for any x of A
A is a subset of B if and only if any x belonging to A implies that x also belongs to B.
An empty set is a subset of ANY set A
Empty = {} = $ \emptyset $ or $ \varnothing $
$ \varnothing \subseteq A $
$ \varnothing \subseteq \varnothing $
Any set is a subset of itself:
$ S \subseteq S $
- Special sets
- N all natural numbers N = {1,2,3,..., \infty}
- Z all integers $ \mathbb{Z} $ = {..., -3,-2,-1,0, 1,2,...}
- The notation $ \mathbb{Z} $ for the set of integers comes from the German word Zahlen, which means "numbers".
- positive integers < 4 = {2}
- Q all rational numbers such as a/b where $ b \neq 0$
- $ Q = \{ \frac{n}{m} | n,m \in \mathbb{R} \ and \ m \ne 0 \} $
- R or $ \mathbb{R} $ all real numbers
In mathematics, a real number $ \mathbb{R} $ is a value of a continuous quantity that can represent a distance along a line (or alternatively, a quantity that can be represented as an infinite decimal expansion). [reference 2]
The listing method and rule of inclusion
- Set representation
- Listing method
- list all elements of the set
- V = {a,e,i,o,u}
- Set builder notation
- example $ Even = \{ 2n | n \in \mathbb{R} \} $
- example $ Odd = \{ 2n+1 | n \in \mathbb{R} \} $
- Q all rational numbers = $ Q = \{ \frac{n}{m} | n,m \in \mathbb{R} \ and \ m \ne 0 \} $
Examples
$ S_1 = \{ 3n | x \in \mathbb{N} \ and \ n < 6 \} \implies $
$ S_1 = \{ 3*1, 3*2, 3*3, 3*4, 3*5 \} \implies $
$ S_1 = \{ 3, 6, 9, 12, 14 \} $
$ S_2 = \{ 2^n | n \in \mathbb{Z} \ and \ 0 \le n \le 4 \} \implies $
$ S_2 = \{ 2^0, 2^1, 2^2, 2^3, 2^4 \} \implies $
$ S_2 = \{ 1, 2, 4, 8, 16 \} $
Important:
$ S_3 = \{ 2^{-n} | n \in \mathbb{Z} \ and \ 0 \le n < 5 \} \implies $
$ S_3 = \{ 2^0, 2^{-1}, 2^{-2}, 2^{-3}, 2^{-4} \} \implies $
$ S_3 = \{ 1, \frac{1}{2}, \frac{1}{4}, \frac{1}{8}, \frac{1}{16} \} $
$ S_4 = \{ \frac{1}{2}, \frac{1}{4}, \frac{1}{6}, \frac{1}{8}, \frac{1}{10} \} \implies $
$ S_3 = \{ \frac{1}{2*N} | n \in \mathbb{Z} \ and \ 1 \le n \le 5 \} $
The powerset of a set
A = {1, 2, 3, 4, 5, 6, 7, 8, 9}
B = {
{1, 2, 3, 4}
{5, 6,}
{1, 2, 3, 4}
{5, 6,}
{7, 8, 9}
}
X = {1, 2, 3, 4}
$ X \subseteq A, \ but \ X \in B $
$ X \subseteq A, \ but \ X \in B $
Read: X is a subset of A, but it is an element of B.
Set S is not an element of S:
$ S = \{1\} \notin S $An empty set is not an element of the empty set:
$ \varnothing \notin \{\} $
An empty set is a subset of the empty set:
$ \{\} = \varnothing \subseteq \varnothing $
- The power set of the set
- definition:
- Given a set S, the powerset of S, written P(S),
is the set containing ALL the subsets of S. - Given S = {1, 2, 3}
- all subsets:
- {}
- {1}, {2},{3}
- {1,2},{1,3},{2,3}
- {1,2,3}
- then P(S)={{},{1}, {2},{3},{1,2},{1,3},{2,3},{1,2,3}}
Cardinality
see reference #3
- then P(S) = $ 2^{|S|} $
- P(S)={{},{1}, {2},{3},{1,2},{1,3},{2,3},{1,2,3}}
- |P(S)| = 2^{|S|} = $ 2^3 = 8 $
- $ |P(A)| = 2^{|A|} = 2^n $
- $ |P(P(A))| = 2^{|P(A)|} = 2^{2^n} $
- $ |P(P(P(A)))| = 2^{|P(P(A))|} = 2^{2^{2^{n}}} $
Powers of 2
$ 2^0 = 1 $
$ 2^1 = 2 $$ 2^2 = 4 $
$ 2^3 = 8 $
$ 2^4 = 16 $
$ 2^5 = 32 $
$ 2^6 = 64 $
$ 2^7 = 128 $
$ 2^8 = 256 $
$ 2^9 = 512 $
$ 2^{10} = 1,024 $
$ 2^{11} = 2,048 $
$ 2^{12} = 4,096 $
$ 2^{13} = 8,192 $
$ 2^{14} = 16,384 $
$ 2^{15} = 32,768 $
$ 2^{16} = 65,536 $
$ 2^{17} = 131,072 $
$ 2^{18} = 262,144 $
$ 2^{19} = 524,288 $
$ 2^{20} = 1,048,576 $
Definition:
Given two sets A and B,
the intersection of A and B, written $ A \cap B $,
contains all the elements in both A and B.
Given two sets A and B,
the set difference, written $ A - B $,
contains all the elements that are in A, but not in B.
Equivalently, two disjoint sets are sets whose intersection is the empty set.
For example,
$ 2^{12} = 4,096 $
$ 2^{13} = 8,192 $
$ 2^{14} = 16,384 $
$ 2^{15} = 32,768 $
$ 2^{16} = 65,536 $
$ 2^{17} = 131,072 $
$ 2^{18} = 262,144 $
$ 2^{19} = 524,288 $
$ 2^{20} = 1,048,576 $
Example:
Given a set A with 12 elements( |A| ).
What is the number of elements (cardinality) in a powerset P(A)?
n = 12
$ |P(A)| = 2^{|A|} = 2^n = 2^{12} = 4096 $
Set Operations
Disjointed Sets (nothing in common)
Definition:
Two sets are disjointed if the intersection is zero.
$$ A \cap B = \varnothing $$
Set Union (all together)
Definition:
Given two sets A and B,
the union of A and B, written $ A \cup B $,
contains all the elements in either A or B.
Given two sets A and B,
the union of A and B, written $ A \cup B $,
contains all the elements in either A or B.
$$ A \cup B = \{x | x \in A \ or \ x \in B \} $$
A = {1, 3, 5}
B = {3, 4, 6}
$ A \cup B $ = {1, 2, 3, 4, 5, 6}
Set Intersection (common)
Given two sets A and B,
the intersection of A and B, written $ A \cap B $,
contains all the elements in both A and B.
$$ A \cap B = \{ x | x \in A \ and \ x \in B \} $$
A = {1, 2, 3}
B = { 3, 5, 6}
$ A \cap B $ = {3}
Set Difference (one but not the other)
Definition:Given two sets A and B,
the set difference, written $ A - B $,
contains all the elements that are in A, but not in B.
$$ A - B = \{ x | x \in A \ and \ x \notin B \} $$
A = {1, 2, 3}
B = { 3, 5, 6}
$ A \cap B $ = {1, 2}
LaTeX \setminus == "$ \setminus $"
Symmetric difference (owned separately)
Definition:
Given two sets A and B,
the symmetric difference, written $ A \oplus B $,
Given two sets A and B,
the symmetric difference, written $ A \oplus B $,
contains all the elements that are in A or in B, but not in both.
$$ A \oplus B = \{ x | ( x \in A \ or \ x \in B ) \ and \ x \notin A \cap B \} $$
$$ A \oplus B = ( A \cup B ) - ( A \cap B ) $$
A = {1, 2, 3}
B = { 3, 5, 6}
$ A \cap B $ = {3}
$ A - B $ = {1, 2}
$ B - A $ = {5, 6}
$ A \oplus B $ = (A-B) + (B-A)
$ A \oplus B $ = {1, 2, 5, 6}
LaTeX symbol substitutes for symmetric difference (see reference 4):
- A \oplus B == "$ A \oplus B $"
- A \triangle B == "$ A \triangle B $"
- A \Theta B == "$ A \Theta B $"
- A \triangledown B == "$ A \triangledown B $"
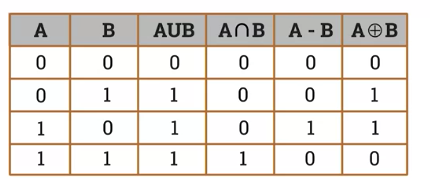
Membership Table
Disjoint Sets
See reference 5.
In mathematics, two sets are said to be disjoint sets if they have no element in common. Equivalently, two disjoint sets are sets whose intersection is the empty set.
For example,
A = {1, 2, 3} and
B = {4, 5, 6} are disjoint sets,
$ A \cup B = \{\} = \varnothing $while {1, 2, 3} and {3, 4, 5} are not disjoint.
The representation of a set using Venn diagrams
See reference 6.
The universal set is marked as U.
The set A is a subset of U, or $ A \subseteq U $.
The complement of a set A, written $ \complement{A} \ or \ \bar{A} \ or \ \overline{A} $,
contains all the elements in the universal set U, but not in set A.
$$ \complement{A} = \overline{A} = U-A $$
$$ \overline{A} \cup A = U $$
$$ \overline{A} \cap A = \varnothing $$
Example:
U = {1, 2, 3, 4, 5, 6, 7, ...} positive integers
A = {2, 4, 6, 8, ...} positive even integers
then,
$ \overline{A} = \{1, 3, 5, 7, 9, ... \}$ positive odd numbers
U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
A = {1, 2, 3, 4, 5}
B = {4, 5, 6, 7, 8, 9, 10}
$ A \cap B $ = {4, 5}
$ \overline{A \cap B} $ = {1, 2, 3, 6, 7, 8, 9, 10}
Example:
U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}
A = {1, 2, 3, 4, 5}
B = {4, 5, 6, 7}
C = {3, 5, 7, 8}
$ D = B \cup C $ = {4, 5, 6, 7, 3, 5, 7, 8} = {3, 4, 5, 6, 7, 8 }
$ A \cap D $ = {3, 4, 5}
$ \overline{A \cap (B \cup C)} $ = $ \overline{A \cap D} $
= {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} - {3, 4, 5} =
= {1, 2, 6, 7, 8, 9, 10}
tip: Use LaTeX \overline{A} = $ \overline{A} $ = long \bar{A} = $ \bar{A} $
Augustus De Morgan's laws
See reference 7.
Definition:
The union of the sets is equal to the intersection of their complements.
$$ \overline{A \cup B} = \bar{A} \cap \bar{B} $$
Definition:
The complement of the intersection of two sets A and B
is equal to the union of their complements.
$$ \overline{ A \cap B } = \bar{A} \cup \bar{B} $$Exercise:
U = {1, 2, 3, 4}
A = {1, 2}
B = {2, 3}
$ \overline{A} $ = {3, 4}
$ \overline{B} $ = {1, 4}
$ \overline{A} \cup \overline{B} $ = {1, 3, 4}
Compliment of the union of compliments:
$ \overline{ \overline{A} \cup \overline{B} } $ = {2}
Intersection, or $ A \cap B $ = {2}
ergo:
$$ \overline{ \overline{A} \cup \overline{ B} } = A \cap B $$
Exercise:
U = {1, 2, 3, 4}
A = {1, 2}
B = {2, 3}
$$ A \cap \overline{ \overline{A} \cup \overline{B}} = ? $$
$ \overline{A} $ = {3, 4}
$ \overline{B} $ = {1, 4}
$ \overline{A} \cup \overline{B} $ = {1, 3, 4}
$ \overline{ \overline{A} \cup \overline{B}} = \{2\} $
$ A \cap \overline{ \overline{A} \cup \overline{B}} = A \cap \{2\} = \{1, 2\} \cap \{2\} = \{2\} $
$ \{2\} = A \cap B $
ergo:
$$ A \cap \overline{ \overline{A} \cup \overline{B}} = A \cap B $$
Exercise:
Given two sets A and B,
What is the complement of the union of their complements?
$$ \overline{ \overline{ A} \cup \overline{ B} } = A \cap B $$
Proof with Vann diagram:
$ \overline{ \overline{ A} \cup \overline{ B} } = ? $
$ \overline{A} = \{3, 4\} $
$ \overline{B} = \{1, 4\} $
$ \overline{ A} \cup \overline{ B} = \{1, 3, 4 \} $
$ \overline{ \{1, 3, 4 \} } = \{2 \}$
$ \overline{ \overline{ A} \cup \overline{ B} } = \{2\} = A \cap B $
$ A - \overline{B} = \{1, 2 \} - \{ 1, 4 \} = {4} = \overline{ A \cup B}$
Exercise:
Set difference of set differences
$$ \overline{ (A-B) - (B-C) } = ? $$
Venn diagram proof:
$ (A-B) = \{1, 3 \} $
$ (B-C) = \{2, 5 \} $
$ \{1, 3 \} - \{2, 5 \} = \{1, 3 \}$
$ \overline{ (A-B) - (B-C) } = \overline{ \{1, 3 \} } = $
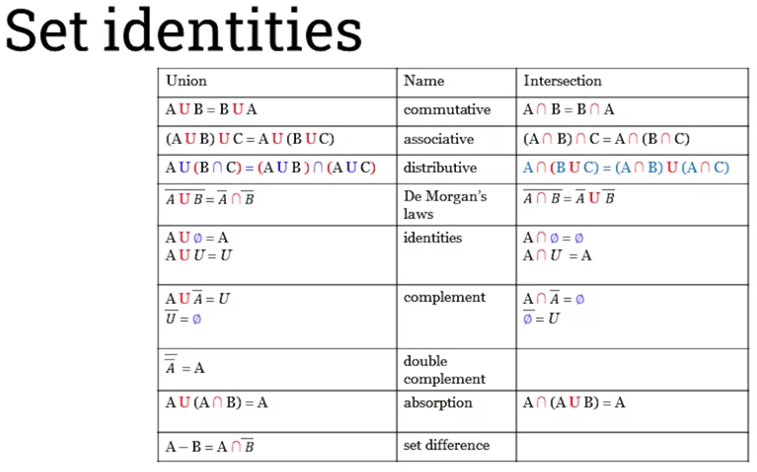
Laws of sets: Commutative, associative, and distributives
See reference 8.
Commutative
Definition:
order does not affect the outcome.
order does not affect the outcome.
Commutative:
- addition 2+3 = 3+2
- multiplication 2*3 = 3*2
- union $ A \cup B = B \cup A $
- intersection $ A \cap B = B \cap A $
- symmetric difference $ A \oplus B = B \oplus A $
Not commutative:
- Subtraction $ 3-1 \neq 1-3 $
- Set difference $ A-B \neq B-A $
Associativity
Definition:
concerns the grouping of elements in an operation.
concerns the grouping of elements in an operation.
Associative:
- addition (a+b)+c = a +(b+c)
- multiplication (a*b)*c = a *(b*c)
- union $ (A \cup B) \cup C = A \cup (B \cup C) $
- intersection $ (A \cap B) \cap C = A \cap (B \cap C) $
- symmetric difference $ (A \oplus B) \oplus C = A \oplus (B \oplus C) $
Not associative
- set difference $ (A - B) - C \neq A - (B - C) $
Distributivity
Definition:
multiplying a sum is equal to multiplying each number and adding the sum
$$ a(b+c) = ac + ac $$
3*(2+5) = 3*2 + 3*5 = 21
$$ A \cup (B \cap C) = (A \cup B) \cap (A \cup C) $$
$$ A \cap (B \cup C) = (A \cap B) \cup (A \cap C) $$
Using set identities to simplify expressions
Prove
$$ \overline{(A \cap B) \cup \overline{B}} = B \cap \overline{A}$$
$ \ \ \ \ \overline{(A \cap B) \cup \overline{B}} = $
$ = \overline{ (A \cap B )} \cap \overline{\overline{B}} $ - De Morgan's law
$ = \overline{ (A \cap B )} \cap B $
$ = ( \overline{A} \cup \overline{B} ) \cap B $ - De Morgan's law
$ = B \cap (\overline{A} \cup \overline{B}) $ - commutative
$ = (B \cap \overline{A}) \cup (B \cap \overline{B}) $ - distributive
$ = (B \cap \overline{A}) \cup \ \varnothing $
$ = B \cap \overline{A} $
Exercise
$ A \cap ( B \cap \overline{A} ) = $
$ = (A \cap B) \cap ( A \cap \overline{A} ) $
$ = (A \cap B) \cap \varnothing = \varnothing $ !
OR
$ A \cap ( B \cap \overline{A} ) = $
$ = A \cap B \cap \overline{A} = $
$ = B \cap A \cap \overline{A} = $
$ = B \cap \varnothing = \varnothing $ !
Exercise
$ \overline{ \overline{A \cup B} \cup \overline{A} } $
$ \overline{A \cup B } = \{4\} $ - Vann diagram
$ \overline{ \{4\} \cup \overline{A} } = $
$ \overline{ \{4\} \cup \{3, 4\} } = \{3, 4 \} = \overline{A} $ !
Exercise
$ \overline{ (A - B) - (B-C) } $
Exercise:
$ \overline{ \overline{A \cup B} \cup \overline{B} } $
$ \overline{A \cup B} = \{ 4 \} $
$ \overline{B} = \{1, 4 \} $
$ \overline{A \cup B} \cup \overline{B} = \{ 1, 4 \} = \overline{B} $
$ \overline{ \overline{A \cup B} \cup \overline{B} } = B = \{2, 3 \} $ !
Exercise:
$ \overline{ A \cup \overline{B} \cup C } \cap \overline{B} $
$ U = \{ 1, 2, 3, 4, 5, 6, 7, 8 \} $
$ \overline{B} = \{ 1, 3, 7, 8 \} $
$ A = \{ 1, 2, 3, 4 \} $
$ C = \{ 3, 4, 6, 7 \} $
$ \overline{ \{ 1, 2, 3, 4 \} \cup \{ 1, 3, 7, 8 \} \cup \{ 3, 4, 6, 7 \}} \cap \{ 1, 3, 7, 8 \} $
$ \overline{ \{ 1, 2, 3, 4, 6, 7, 8 \} } \cap \{ 1, 3, 7, 8 \} $
$ \{ 5, 6 \} \cap \{ 1, 3, 7, 8 \} = \varnothing $Exercise:
$ A \cup ( B \cup \overline{A}) = $
$ A \cup B \cup \overline{A} = $
$ B \cup A \cup \overline{A} = $
$ B \cup \varnothing = B$
Q.E.D.
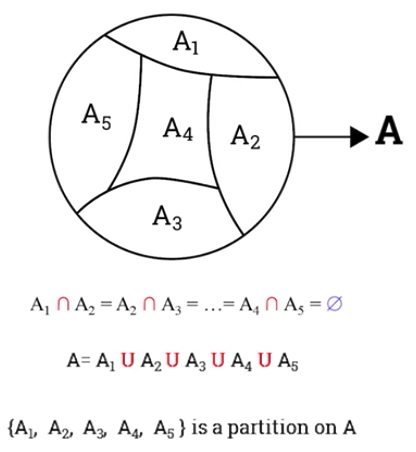
Partition of a set
See reference 9.
Definition:
A partition of set A,
is a set of subsets $ A_i $ of A such that:
all the subsets $ A_i $ are disjointed,
all the subsets $ A_i $ are disjointed,
and the union of all subsets $ A_i $ is equal to A.
Exercise
Hint: Use the inclusion-exclusion principle (IEP):
$ | A \cup B | = | A | + | B | - | A \cap B | $
The formula expresses the fact that the sum of the sizes of the two sets may be too large since some elements may be counted twice. The double-counted elements are those in the intersection of the two sets and the count is corrected by subtracting the size of the intersection.
https://en.wikipedia.org/wiki/Inclusion%E2%80%93exclusion_principle
$ | A \cup B | = | A | + | B | - | A \cap B | $
The formula expresses the fact that the sum of the sizes of the two sets may be too large since some elements may be counted twice. The double-counted elements are those in the intersection of the two sets and the count is corrected by subtracting the size of the intersection.
https://en.wikipedia.org/wiki/Inclusion%E2%80%93exclusion_principle
Given three sets A, B, and C, prove that:
I could not find the use for associativity of the union, so I just show it here:
$ | C \cup (A \cup B) | = | A\cup B \cup C | = $
$ | C \cup (A \cup B) | = | A\cup B \cup C | = $
1. Using IEP, split above:
$ = | A\cup B | + | C | - | (A \cup B) \cap C | = $
2. Using IEP, split $ | A\cup B | $ above:
$ | A \cup B | = | A | + | B | - | A \cap B | $
3. Combine the two terms:
$ = | A | + | B | - | A \cap B | + | C | - | (A \cup B) \cap C | = $
4. Use associativity of addition for arranging the terms:
$ = \color{green}{ | A | + | B | + | C | - | A \cap B | } - | (A \cup B) \cap C | = $5. Using distributivity of the intersection, split the last union:
$ | (A \cup B) \cap C | = | ( A \cap C ) \cup ( A \cap B) | $
6. Using IEP, split the term
$ = | ( A \cap C ) \cup ( A \cap B) | = | A \cap C | + | A \cap B | - | A \cap C) | \cap | A \cap B |$
7. Combine the terms
$ = \color{green}{ | A | + | B | + | C | - | A \cap B | - | A \cap C | + | A \cap B | } - | A \cap C | \cap | A \cap B | $
8. Using commutativity of the intersection law (clearly proven by Vann diagram):
$ | A \cap C | \cap | A \cap B | = | A \cap B \cap C | $
9. Combining the terms:
$ = \color{green}{| A | + | B | + | C | - | A \cap B | - | A \cap C | + | A \cap B | - | A \cap B \cap C | } $
Q.E.D.
Visual proof of the same:
$ | A\cup B \cup C | = $ using IEP, see Venn diagram below for reference
$ = | A | + | B | + | C | $ - accounts for all sets, but double counts subsets 2, 3, 6 and triple counts subset 4resulting in:
$ = | S_1 | + | S_2 | + | S_2 | + | S_3 | + | S_3 | + | S_4 | + | S_4 | + | S_4 | + | S_6 | + | S_6 | $
to correct that:
$ - | A \cap B | $ remove one double counted subsets 2, 4
$ - | A \cap C | $ remove one double counted subsets 3, 4
$ - | B \cap C | $ remove one double counted subsets 6, 4
but at this point, we removed all three $ S_4 $ so we have to add:
$ + | A \cap B \cap C |$ intersection of all set resulting in subset 4
$ = | A | + | B | + | C | - | A \cap B | - | A \cap C | - | B\cap C | + | A \cap B \cap C | $
E.Q.D.
Exercise:
Given A (even numbers) and B (odd numbers) which are subsets to the universal Integer set U,
$$ U = \{x: x \in \mathbb{Z} \ and \ 0 \leq x < 20 \} $$Therefore:
$ U = \{0, 1, 2, 3, ..., 18, 19 \} $
$ A = \{0, 2, 4, 6, 8, 10, 12, 14, 16, 18 \} $ assuming even numbers include zero 0
$ B = \{1, 3, 5, 7, 9, 11, 13, 15, 17, 19 \} $
$ A\cup B = U $ $ A\cap B = \varnothing $ empty set
$ \overline{B} = A $
Use the listing method to list the elements of the following sets:
$ A \cap \overline{B} = \{0, 2, 4, ..., 16, 18 \} \cap \{ 0, 2, 4, ..., 16, 18 \} = A = \{ 0, 2, 4, ..., 16, 18 \} $$ \overline{A \cap B} = \overline{ \varnothing } = \overline{ \{\} } = U = \{0, 1, 2, 3, ..., 18, 19 \} $
Use the listing method to list the elements of the following sets:
$ A \cap \overline{B} = \{0, 2, 4, ..., 16, 18 \} \cap \{ 0, 2, 4, ..., 16, 18 \} = A = \{ 0, 2, 4, ..., 16, 18 \} $
$ \overline{A \cup B } = \overline{ U } = \overline{\{0, 1, 2, 3, ..., 18, 19 \}} = \{\} = \varnothing $
$ \overline{A \oplus B} = U - (A \cup B) + ( A \cap B) = \{\} = \varnothing $
Peer reviews
Read Book
Discrete Mathematics with Applications
Thomas Koshy
https://ebookcentral.proquest.com/lib/londonww/detail.action?docID=294091#
pp.70-71, 71-73, and 78-86.
Please also complete the following exercises:
pp.93, exercises 5–14, 27-32, and 57-60.
Review Problem Sheet
TODO: review and documentCartesian Product of A and B
Summative Quiz
TODO
Webinar
https://www.coursera.org/learn/uol-discrete-mathematics/lecture/B7F94/webinar
References
- https://en.wikipedia.org/wiki/Set_(mathematics)
- https://en.wikipedia.org/wiki/Real_number
- https://en.wikipedia.org/wiki/Cardinality
- https://proofwiki.org/wiki/Symbols:Set_Theory/Symmetric_Difference
- https://en.wikipedia.org/wiki/Disjoint_sets
- https://en.wikipedia.org/wiki/Venn_diagram
- https://en.wikipedia.org/wiki/De_Morgan%27s_laws
- https://www.coursera.org/learn/uol-discrete-mathematics/lecture/QEPbf/1-205-laws-of-sets-commutative-associative-and-distributives
- https://www.coursera.org/learn/uol-discrete-mathematics/lecture/FuScz/1-207-partition-of-a-set
- Discrete Mathematics with Applications - Thomas Koshy