Machine Learning with Python
All images are copyrighted by IBM.
Objective:
We have to find the best parameters $ \theta_0 $ and $ \theta_1 $ to minimize the MSE.
$$
\theta_1 =
\frac{
\sum_{i=1} ^{s}
\left( x_i - \bar{x} \right)
\left( y_i - \bar{y} \right)
}{
\sum_{i=1} ^{s}
\left( x_i - \bar{x} \right)^2
}
$$
where:
Conclusions for Linear Regression:
$$
MAE =
\frac{1}{n}
\sum_{j=1}^{n}
| \hspace{0.5em}
y_j - \hat{y}_j
\hspace{0.5em} |
$$
$$
RMSE =
\sqrt{
\frac{1}{n}
\sum_{j=1}^{n}
\left(
y_j - \hat{y}_j
\right)^2
}
$$
Relative Absolute Error (RAE):
RAE =
\frac
{
\sum_{j=1}^{n}
|
y_j - \hat{y}_j
|
}{
\sum_{j=1}^{n}
|
y_j - \bar{y}
|
}
$$
RAE =
\frac
{
\sum_{j=1}^{n}
\left(
y_j - \hat{y}_j
\right)^2
}{
\sum_{j=1}^{n}
\left(
y_j - \bar{y}
\right)^2
}
$$
You should do your own investigation of when to use each error estimation method.
When should I use Multiple Linear Regression?
- When there are multiple dependent variables and EACH independent variable has a linear correlation with the dependent variable.
$$
X = \begin{bmatrix}
1 \\
x_1 \\
x_2 \\
x_3 \\
\vdots
\end{bmatrix}
$$
Definitions:
Machine learning is a subfield of computer science that gives "computers the ability to learn without being explicitly programmed."
Machine Learning tries to train on a large quantity of data and derive solutions to cases not encountered during the training.
AI, a subset of machine Learning, tries to make computers intelligent with vision, language, creativity, etc.
Deep Learning is a subset of AI, where computers learn and make decisions on their own.
The course covers:
- Regression / Estimation
- predicting continuous values
- Classification
- predicting the item class or category
- Clustering
- finding the structure of the data, summarization
- Association
- finding co-occurring items or events
- Anomaly detection
- discovering abnormal or unusual cases
- Sequence mining
- predicting next events; e.g. click stream (Markov Model, HMM)
- Dimension Reduction
- reducing the size of the data (PCA)
- Recommendation Systems
- discovering preferences
Software tools:
- Scikit Learn
- algorithms for machine learning
- SciPy
- signal processing, optimization, statistics, etc.
- NumPy
- arrays, dictionaries, data structures, etc.
- MatPlotLib
- 2D and 3D plotting
- Pandas
- high-performance data structures, data importing, manipulation, and analysis, numerical tables and time-series
Projects:
- Cancer detection
- Economic trends
- Customer churn
- Recommendation engines
- more
Example:
Benign or malignant?
Pipeline:
- Data Preprocessing
- Train vs Test data split
- Algorithm Setup
- Model Fitting
- Prediction
- Evaluation
- Model Export
scikit-learn functions
Supervised vs Unsupervised Algorithms
Supervised learning is using a "labeled" data set.
data column = feature
data row = observation
There are 2 types of "supervised" learning:
- Classification
- Regression
The unsupervised model draws conclusions on unlabeled data.
Unsupervised techniques:
- Dimension reduction
- Density estimation
- Market basket analysis
- Clustering
- Discovering structure
- Summarization
- Anomaly detection
Linear Regression
Introduction to Regression
https://www.coursera.org/learn/machine-learning-with-python/lecture/AVIIM/introduction-to-regression
Simple Linear Regression
Data:
- X: independent variable
- explanatory variables
- can be measured on a categorical or continuous scale
- Y: dependent variable
- which we try to predict
- needs to be continuous and cannot be a discrete value
Types of regression models:
- Simple regression (1 feature vs the dependent variable)
- simple linear regression
- simple non-linear regression
- Multiple regression (comparing 2+ features)
- multiple linear regression
- multiple non-linear regression
Applications:
- sales forecasting
- satisfaction analysis
- price estimation
- employment income
Regression algorithms:
- ordinal regression
- poison regression
- fast forest quantile regression
- Linear, Polynomial, Lasso, Stepwise, Ridge regression
- Bayesian linear regression
- Neural network regression
- Boosted decision tree regression
- KNN (K-nearest neighbors)
Fit line:
- it is a polynomial written as $ ŷ=\theta_0 + \theta_1 x_1 $
- where
- y is a particular, observed, dependent variable (i.e. emissions )
- $ \hat{y} $, or y "hat" is the response variable or predicted value (ideal value on fitted regression line)
- $ \theta_0 $ y-intercept of the line
- $ \theta_1 $ is the slope or gradient of the line
- $ x_1 $ is the independent variable or a single predictor (i.e engine size in liters)
- $ \theta_0 $ and $ \theta_1 $ are also called the coefficients of the equation
Error
The difference between the ŷ and y is the error.
The mean of the squared sum of errors (differences) formula:
$$ MSE = \frac{1}{n} \sum_{i=1} ^{n} \left( y_i - ŷ_i \right)^2 $$
We have to find the best parameters $ \theta_0 $ and $ \theta_1 $ to minimize the MSE.
Options to find $ \theta_0 $ and $ \theta_1 $:
- mathematical approach
- optimization approach
\theta_1 =
\frac{
\sum_{i=1} ^{s}
\left( x_i - \bar{x} \right)
\left( y_i - \bar{y} \right)
}{
\sum_{i=1} ^{s}
\left( x_i - \bar{x} \right)^2
}
$$
- s = n , or number of observations (rows in the table)
- $ \bar{x} = \frac{\sum_{i=1} ^{n} \left( x_i \right) }{n} $ or, x "bar" is mean of x
- $ \bar{y} = \frac{\sum_{i=1} ^{n} \left( y_i \right) }{n} $ or, y "bar" is mean of y
Conclusions for Linear Regression:
- very fast
- no parameter tuning
- easy to interpret
Model Evaluation in Regression Models
Calculate the Error:
$$
\hat{y} =
\frac{1}{n}
\sum_{j=1}^{n}
| y_j - \hat{y}_j |
$$
$$
\hat{y} =
\frac{1}{n}
\sum_{j=1}^{n}
| y_j - \hat{y}_j |
$$
Understanding the difference:
Wrong "Out of Sample Accuracy" is the percentage of correct predictions that the model makes on data that the model has NOT been trained on.
- train and test on the same data
- High training accuracy is not necessarily a good thing
- Overfitting
- memorized the input to output data and produced a non-generalized model
- aka: rote learning
- provides bad results for the input data that the model was not trained on
- train and test on the split data
"Out of Sample Accuracy" is the accuracy of an overly trained model (which may capture noise and produced a non-generalized model)
Evaluation:
- testing on the portion of the test data (not split, not randomized)
- high "training accuracy"
- low "out of sample" accuracy
- testing on the split data (randomized)
- more accurate evaluation for "out of sample" accuracy
- highly dependent on which data is selected
K-fold cross-validation
Evaluation Metrics in Regression Models
https://www.coursera.org/learn/machine-learning-with-python/lecture/5SxtZ/evaluation-metrics-in-regression-models
Error definition:
The difference between observed data points ($ y_i $) and the fitted trend (regression) line values ($ \hat{y} $).
Mean Absolute Error (MAE):
- easy to understand
MAE =
\frac{1}{n}
\sum_{j=1}^{n}
| \hspace{0.5em}
y_j - \hat{y}_j
\hspace{0.5em} |
$$
Mean Squared Error (MSE):
- more commonly used
- stresses the large errors, exponentially increasing them (hence $ error^2 $)
$$
MSE =
\frac{1}{n}
\sum_{j=1}^{n}
\left(
y_j - \hat{y}_j
\right)^2
$$
MSE =
\frac{1}{n}
\sum_{j=1}^{n}
\left(
y_j - \hat{y}_j
\right)^2
$$
Root Mean Squared Error (RMSE):
- MOST commonly used
- interpretable in the same units as the response vector, or y-units, easy to relate the information
RMSE =
\sqrt{
\frac{1}{n}
\sum_{j=1}^{n}
\left(
y_j - \hat{y}_j
\right)^2
}
$$
Relative Absolute Error (RAE):
- aka: residual sum of squares
- normalizes the value by dividing the derived error by the mean error
RAE =
\frac
{
\sum_{j=1}^{n}
|
y_j - \hat{y}_j
|
}{
\sum_{j=1}^{n}
|
y_j - \bar{y}
|
}
$$
Relative Absolute Error (RSE):
- widely used by the data community to calculate $ R^2 $
- $ R^2 = 1- RSE $
- it is a popular metric of your model: shows how close the data values are to the fitted regression line
- the higher the $ R^2 $ the better the model fits your data
RAE =
\frac
{
\sum_{j=1}^{n}
\left(
y_j - \hat{y}_j
\right)^2
}{
\sum_{j=1}^{n}
\left(
y_j - \bar{y}
\right)^2
}
$$
Lab: Simple Linear Regression (1hr)
At this point, I decided that adding about 1 hour of setup work will be beneficial in the long run:
- create a private GitHub repo for the University of London CS that will include a directory for this certification:
https://github.com/UkiDLucas/UoL_CS - Install Anaconda Python environment with Jupyter Notebook, etc.
https://uki.blogspot.com/2018/10/conda-environment-as-jupyter-notebook.html - locally this looks like this:
_REPOS/UoL_CS/IBM_AI_Eng/ML_Python/ML0101EN-Reg-Simple-Linear-Regression-Co2.ipynb
Multiple Linear Regression
https://www.coursera.org/learn/machine-learning-with-python/lecture/0y8Cq/multiple-linear-regression
- When there are multiple dependent variables and EACH independent variable has a linear correlation with the dependent variable.
- Most of the applications of Linear Regression use multiple variables.
$$ \hat{y} = \theta_0 + \theta_1 x_1 + \theta_2 x_2 + ... + \theta_n x_n $$
$$ \hat{y} = \theta^T X $$
$$ \theta^T = \left[ \theta_0, \theta_1, \theta_2, ... \right] $$
X = \begin{bmatrix}
1 \\
x_1 \\
x_2 \\
x_3 \\
\vdots
\end{bmatrix}
$$
Where:
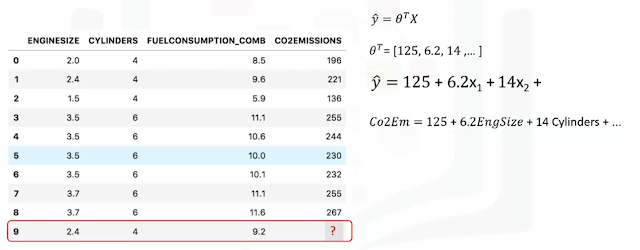
- $ \hat{y} $ is a "dot" product of two vectors $ \theta^T X $,
- in one-dimensional space, it is an equation of a line
- in two-dimensional space, it is a plane
- in multi-dimensional space, it is a hyper-plane
- $ \theta^T $ is the n-by-1 vector of unknown parameters in the multi-dimensional space,
- traditionally it is shown as transpose $ \theta $,
- it is also called:
- the vector of parameters,
- vector of coefficients,
- or the weight vector of the regression equation
- T indicates "transpose" (see reference 4)
- X is the feature set vector
- the first element of X is 1, an intercept, or bias parameter
We have to optimize the parameters $ \theta $ in $ \hat{y} = \theta^T X $ to result in the fewest errors.
- For example, let's assume:
- for a given set of parameters we get the result for row 1:
- $ \hat{y}_1 $ = 140
- from the observation dataset, we see
- $ y_1 $ = 196
- hence:
- $ y_1 - \hat{y} $ = 196 -140 = 56
- which is called residual error for a single observation
- or distance from the regression line
We can use the Means Square Error formula to calculate the error for all the observations:
$$
MSE =
\frac{1}{n}
\sum_{j=1}^{n}
\left(
y_j - \hat{y}_j
\right)^2
$$
MSE =
\frac{1}{n}
\sum_{j=1}^{n}
\left(
y_j - \hat{y}_j
\right)^2
$$
Methods to find optimal coefficients:
- Ordinary Least Squares
- Linear algebra operations
- it takes a long time for large datasets (10k+ rows)
- Scikit-learn uses the plain Ordinary Least Squares method
- Optimization Approach
- Gradient Decent
- a proper approach for the large data sets
Concerns:
- multiple linear regression may give you a better predictive model
- avoid overfitting
- convert variables to continuous numbers
- analyze the relationships between dependent and independent variables
- use scatterplots to check for linearity, if there is no dependency then do not use it
Lab: Multiple Linear Regression
Non-Linear (Polynomial) Regression
Non-linear regression is a method to model the non-linear relationship between the independent variables 𝑥x and the dependent variable 𝑦y. Essentially any relationship that is not linear can be termed as non-linear and is usually represented by the polynomial of 𝑘k degrees (maximum power of 𝑥x). For example:
$$ 𝑦 = 𝑎𝑥^3 + 𝑏𝑥^2 + 𝑐𝑥 + 𝑑 $$
Non-linear functions can have elements like exponentials, logarithms, fractions, etc. For example:
$$ 𝑦 = log(𝑥) $$
$$ \hat{y} = \frac{ \theta_0 }{ 1 + \theta_1^ \left( x - \theta_2 \right) } $$
We can have a function that's even more complicated such as :
$$ 𝑦 = log(𝑎𝑥^3 + 𝑏𝑥^2 + 𝑐𝑥 + 𝑑) $$
How do we know whether the problem is linear or non-linear?
- inspect data visually
- fit non-linear model
- transform your data
Exponential (hockey stick) functions:
$$ \hat{y} =
\theta_0
+ \theta_1
\theta_2^x
$$
\theta_0
+ \theta_1
\theta_2^x
$$
Logarithmic (inverse hockey stick) Regression
$$ \hat{y} =
\log{
\left(
\theta_0
+ \theta_1 x
+ \theta_2 x^2
+ \theta_3 x^3
\right)
}
$$
\log{
\left(
\theta_0
+ \theta_1 x
+ \theta_2 x^2
+ \theta_3 x^3
\right)
}
$$
In the case below,
$$ \hat{y} =
\theta_0
+ \theta_1
\log{x}
$$
\theta_0
+ \theta_1
\log{x}
$$
Quadratic (parabolic) Regression
$$ \hat{y} =
\theta_0
+ \theta_1 x
+ \theta_2 x^2
$$
\theta_0
+ \theta_1 x
+ \theta_2 x^2
$$
in the example below:
$$ \hat{y} =
\theta_0 * 0
+ \theta_1 x * 0
+ \theta_2 x^2
$$
\theta_0 * 0
+ \theta_1 x * 0
+ \theta_2 x^2
$$
Cubic (s-curve) Polynomial (3rd degree) Regression
$$ \hat{y} =
\theta_0
+ \theta_1 x
+ \theta_2 x^2
+ \theta_3 x^3
$$
\theta_0
+ \theta_1 x
+ \theta_2 x^2
+ \theta_3 x^3
$$
Logistic Regression (sigmoid curve)
generic:
$$ Y = a + \frac{b}{1+ c^{(X-d)}} $$
Specific below:
$$ Y = \hat{y} = 0 + \frac{-3}{1 + 3^{(X-2)}} $$
Given the 3rd-degree polynomial equation:
$$
x_1 = x \\
x_2 = x^2 \\
x_3 = x^3
$$
x_1 = x \\
x_2 = x^2 \\
x_3 = x^3
$$
The model is converted to a simple (special case of multiple) linear regression:
$$ \hat{y} =
\theta_0
+ \theta_1 x_1
+ \theta_2 x_2
+ \theta_3 x_3
$$
\theta_0
+ \theta_1 x_1
+ \theta_2 x_2
+ \theta_3 x_3
$$
Least Squares is a method of estimating unknown parameters in a linear regression model by
minimizing the sum of the squares of the differences between $ y $ and $\hat{y} $.
minimizing the sum of the squares of the differences between $ y $ and $\hat{y} $.
Please continue to Classification:
https://uki.blogspot.com/2022/10/classification.html
https://uki.blogspot.com/2022/10/classification.html
References
- https://oeis.org/wiki/List_of_LaTeX_mathematical_symbols
- https://tex.stackexchange.com/questions/13865/how-to-use-latex-on-blogspot
- Special Characters (i.e. Greek) LaTex https://uki.blogspot.com/search/label/Jupyther%20Lab
- https://en.wikipedia.org/wiki/Transpose
- https://www.atqed.com/latex-column-vector
